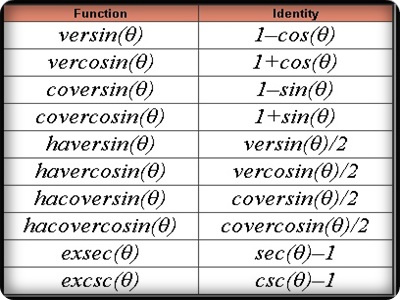
Para Pembaca Berita Info Pernahkah mendengar ? Versine, Vercosine, Coversine, Covercosine, Exsecant, Excosecant, Haversince, Havercosine, Hacoversine, Hacovercosine? Pastinya bukan nama obat, apalagi nama obat kulit.Dan juga pastinya nama-nama itu tidak mewakili seluruh bagian matematika yang di lewatkan di sekolah. Itu semua hanyalah nama yang ramah untuk kombinasi dasar dari tiga fungsi trigonometri dasar. Berikut identitas mereka:
Dalam dunia matematika, trigonometri adalah cabang yang mempelajari hubungan antara sudut dan sisi dalam segitiga. Namun, ada beberapa fungsi trigonometri yang kurang dikenal dan jarang digunakan oleh banyak orang. Dalam blog ini, kita akan menjelaj dan memb fungsi-fungsi tersebut yang dikenal sebagai versine vercosine, coversine, covercosine, exsecant, excosecant, haversine, havercosine, hacoversine, dan hacovercosine. Mari kita pelajari fungsi-fungsi ini dan bagaimana mereka dapat digunakan dalam pemecahan masalah matematika.
Bagian 1: Mengenal Fungsi Versine
Fungsi versine adalah fungsi trigonometri yang jarang digunakan dalam matematika modern. Fungsi ini didefinisikan sebagai 1 minus kosinus dari suatu sudut. Dalam notasi matematika, versine dari sudut t ditulis sebagai vers(t) atau ver(t).
Versine dapat digunakan dalam beberapa aplikasi seperti navigasi maritim dan astronomi. Misalnya, dalam navigasi maritim, versine digunakan untuk menghitung jarak antara dua titik di permukaan bumi berdasarkan perbedaan lintang. Namun, karena kemajuan teknologi dan penggunaan metode yang lebih efisien seperti menggunakan GPS, penggunaan versine dalam aplikasi praktis semakin jarang.
Bagian 2: Menjelajahi Fungsi Vercosine
Fungsi vercosine adalah kebalikan dari fungsi versine. Dalam notasi matematika, vercosine dari sudut t ditulis sebagai vercos(t) atau vec(t). Fungsi ini didefinisikan sebagai 1 minus sinus dari suatu sudut.
Vercosine juga memiliki beberapa aplikasi dalam trigonometri sferis dan navigasi. Dalam trigonometri sferis, vercosine digunakan untuk menghitung jarak antara dua titik pada permukaan bola. Namun, seperti halnya dengan versine, penggunaan vercosine secara praktis semakin berkurang dengan kemajuan teknologi.
Bagian 3: Mempelajari Fungsi Coversine
Fungsi coversine adalah fungsi trigonometri lain yang kurang umum. Coversine dari sudut t didefinisikan sebagai 1 minus sinus dari sudut tersebut. Dalam notasi matematika, coversine dari sudut t ditulis sebagai covers(t) atau cov(t).
Coversine juga memiliki beberapa aplikasi dalam trigonometri sferis dan navigasi. Sebagai contoh, dalam astronomi, coversine digunakan untuk menghitung jarak antara dua bintang berdasarkan perbedaan deklinasi. Namun, seperti halnya dengan versine dan vercosine, penggunaan coversine dalam aplikasi praktis semakin berkurang.
Bagian 4: Mengenal Fungsi Covercosine
Fungsi covercosine adalah kebalikan dari fungsi coversine. Dalam notasi matematika, covercosine dari sudut t ditulis sebagai covercos(t) atau coc(t). Fungsi ini didefinisikan sebagai 1 minus kosinus dari suatu sudut.
Covercosine juga memiliki beberapa aplikasi dalam trigonometri sferis dan navigasi. Misalnya, dalam pemetaan bumi atau pemodelan iklim global, covercosine digunakan untuk menghitung perubahan suhu berdasarkan garis lintang. Namun, penggunaan covercosine secara praktis semakin berkurang seiring dengan kemajuan teknologi dan metode perhitungan yang lebih efisien.
Bagian 5: Menjelajahi Fungsi Exsecant
Fungsi exsecant adalah fungsi trigonometri yang kurang umum dan jarang digunakan. Exsecant dari sudut t didefinisikan sebagai 1 dibagi oleh kosinus dari sudut tersebut. Dalam notasi matematika, exsecant dari sudut t ditulis sebagai exsec(t) atau exc(t).
Exsecant dapat digunakan dalam beberapa aplikasi seperti astronomi dan navigasi. Sebagai contoh, dalam astronomi bola langit, exsecant digunakan untuk menghitung lintasan orbit benda langit berdasarkan elemen orbitnya. Namun, penggunaan exsecant dalam aplikasi praktis semakin berkurang seiring dengan kemajuan teknologi dan metode perhitungan yang lebih efisien.
Bagian 6: Mempelajari Fungsi Excosecant
Fungsi excosecant adalah kebalikan dari fungsi exsecant. Dalam notasi matematika, excosecant dari sudut t ditulis sebagai excosec(t) atau excc(t). Fungsi ini didefinisikan sebagai 1 dibagi oleh sinus dari suatu sudut.
Excosecant juga memiliki beberapa aplikasi dalam trigonometri sferis dan navigasi. Sebagai contoh, dalam navigasi maritim, excosecant digunakan untuk menghitung jarak antara dua titik di permukaan bumi berdasarkan perbedaan garis lintang. Namun, penggunaan excosecant secara praktis semakin berkurang dengan kemajuan teknologi dan metode perhitungan yang lebih efisien.
Bagian 7: Mengenal Fungsi Haversine
Fungsi haversine adalah fungsi trigonometri yang kurang dikenal tetapi memiliki beberapa aplikasi penting dalam matematika dan ilmu pengetahuan. Haversine dari sudut t didefinisikan sebagai setengah dari kuadrat sinus setengah sudut tersebut. Dalam notasi matematika, haversine dari sudut t ditulis sebagai hav(t).
Hine digunakan luas dalam navigasi dan pemetaan bumi Misalnya, dalam navigasi pesawat terbang atau kapal laut, haversine digunakan untuk menghit jarak melasi bola langit antara dua tit dengan mengingat bahwa permukaan bumi dapat dianggap sebagai bola. Penggunaan haversine juga penting dalam pemodelan iklim global dan analisis data geospasial.
Bagian 8: Mempelajari Fungsi Havercosine
Fungsi havercosine adalah kebalikan dari fungsi haversine. Dalam notasi matematika, havercosine dari sudut t ditulis sebagai havercos(t). Fungsi ini didefinisikan sebagai setengah dari kuadrat kosinus setengah sudut tersebut.
Havercosine juga memiliki beberapa aplikasi dalam matematika terapan dan ilmu pengetahuan. Misalnya, dalam pemodelan pergerakan atmosfer atau aliran air di permukaan bumi, havercosine digunakan untuk menghitung gaya gradien berdasarkan perbedaan elevasi antara dua titik. Penggunaan havercosine juga penting dalam pemodelan topografi dan analisis data geospasial.
Bagian 9: Menjelajahi Fungsi Hacoversine
Fungsi hacoversine adalah fungsi trigonometri lain yang jarang digunakan tetapi memiliki beberapa aplikasi penting dalam matematika dan ilmu pengetahuan. Hacoversine dari sudut t didefinisikan sebagai setengah dari kuadrat coversin setengah sudut tersebut. Dalam notasi matematika, hacoversine dari sudut t ditulis sebagai hacovers(t).
Hacoversine sering digunakan dalam astronomi dan navigasi sferis. Misalnya, dalam pemetaan bintang atau perencanaan misi luar angkasa, hacoversine digunakan untuk menghitung jarak antara dua benda langit berdasarkan perbedaan deklinasi. Penggunaan hacoversine juga penting dalam pemodelan kedudukan bulan dan matahari serta analisis data astronomi.
Bagian 10: Mempelajari Fungsi Hacovercosine
Fungsi hacovercosine adalah kebalikan dari fungsi hacoversine. Dalam notasi matematika, hacovercosine dari sudut t ditulis sebagai hacovercos(t). Fungsi ini didefinisikan sebagai setengah dari kuadrat covercosin setengah sudut tersebut.
Hacovercosine juga memiliki beberapa aplikasi dalam ilmu pengetahuan dan matematika terapan. Misalnya, dalam pemodelan pergerakan partikel di medan elektromagnetik atau medan gravitasi, hacovercosine digunakan untuk menghitung gaya yang bekerja pada partikel berdasarkan perbedaan energi potensial. Penggunaan hacovercosine juga penting dalam pemodelan fisika partikel dan analisis data ilmiah.
Dengan mengeksplorasi fungsi-fungsi trigonometri yang kurang dikenal ini, kita dapat memperluas pemahaman kita tentang matematika dan melihat bagaimana konsep-konsep ini dapat diterapkan dalam berbagai bidang ilmu pengetahuan dan teknologi. Meskipun penggunaannya mungkin terbatas saat ini karena kemajuan teknologi dan metode perhitungan yang lebih efisien, pengetahuan tentang fungsi-fungsi ini masih penting untuk memahami dasar-dasar trigonometri dan memecahkan masalah yang lebih kompleks di masa depan.

Rumus Haversine
Versine adalah fungsi trigonometri yang cukup jelas untuk didefinisikan dan tampaknya telah digunakan sejak 400 Masehi di India. Tapi haversine mungkin lebih penting dalam sejarah yang lebih baru, ketika digunakan dalam navigasi. Rumus haversine adalah cara yang sangat akurat untuk menghitung jarak antara dua titik pada permukaan bola menggunakan garis lintang dan garis bujur dari dua titik. Rumus haversine adalah formulasi ulang dari hukum cosinus bola, tetapi formulasi dalam istilah haversine lebih berguna untuk sudut dan jarak kecil. (Di sisi lain, rumus haversine tidak melakukan pekerjaan yang sangat baik dengan sudut yang mendekati 90 derajat, tetapi hukum bola cosinus menanganinya dengan baik.) Rumus haversine dapat menghasilkan hasil yang akurat tanpa memerlukan operasi komputasi yang mahal kuadrat dan akar kuadrat. Baru-baru ini pada tahun 1984, majalah astronomi amatir Sky & Telescope memuji rumus haversine, yang tidak hanya berguna untuk navigasi terestrial tetapi juga untuk perhitungan langit (Celestial).Dalam tabel fungsi trigonometri rahasia, "ha" jelas berarti setengah; nilai haversine adalah setengah dari nilai versine, misalnya. "Co" berarti mengambil fungsi yang sama tetapi dengan sudut komplementer. (Sudut komplementer berjumlah 90 derajat. Dalam segitiga siku-siku, dua sudut tidak siku-siku saling komplementer.) Misalnya, kosinus suatu sudut juga merupakan sinus sudut komplementer. Demikian pula, coversin adalah versi dari sudut komplementer.Jika "co" dalam definisi itu berarti sudut komplementer, maka vercosine akan sama dengan coversine, padahal bukan. Sebaliknya, vercosine adalah versine dari sudut tambahan (sudut tambahan berjumlah 180 derajat), bukan sudut pelengkap. Selain definisi sebagai 1-cos(θ) dan 1+cos(θ), versine dan vercosine dapat didefinisikan sebagai versin(θ)=2sin2(θ/2) dan vercos(θ)=2cos2(θ/2 ). Dalam kasus versine, saya yakin definisi yang melibatkan cos(θ) lebih tua dari definisi yang melibatkan sinus kuadrat.